In this blog post, I will give an introduction to a hashing methodology called Linear Hashing.
Hash Table Detour
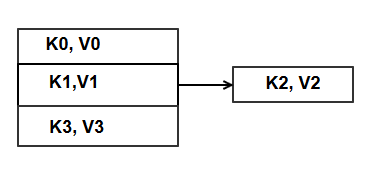
A hash table is a well known in-memory structure that supports key-value access with lookup cost being amortized O(1). The hash table is just an array, and each location/index in the array stores a <KEY,VALUE> item. The data structure is accompanied by a hashing function that maps a given key K to the table index that stores the value V for this key.
It is quite possible that multiple keys hash to the same location (aka bucket) in the hash table. If this is the case we have a collision, and this affects the performance of both insert() and lookup() operations in the hash table. Typical collision resolution strategy is chaining where each bucket in the hash table array has a chain (basically a linked list) of overflow buckets. Let’s say we wish to insert key K2 at bucket B ; B = h(K2) where “h” is the hash function.
If there is a collision at bucket B, implying some other <K1, V1> pair already exists there, following steps are followed to store the desired new item <K2 ,V2>.
- Create a new overflow bucket ; allocate memory for the bucket structure.
- Store the <K2, V2 > pair there.
- Link this overflow bucket to the chain of bucket B.
The length of the chain at any given bucket will obviously impact the cost of lookup() for keys hashing to that bucket because it requires a search through the chain. It will usually not affect the cost of insertion since a new item can always be inserted by creating and linking an overflow bucket at the head of the chain. But, if some sort of ordering on keys is required, then cost of insert() will also increase.
So it is imperative that hash table is of optimal size. An under sized hash table can quickly lead to degradation in performance if the per-bucket chain length is high. On the other hand, if we over provision the memory for hash table, we suffer space wastage. Hence, dynamically changing the hash table size by adding more number of buckets, and rehashing the existing set of KV pairs using the new table size is an important operation on the hash table.
Linear Hashing
Linear Hashing technique is a dynamic hashing scheme. It allows the hash table size to grow in a linear fashion ; one bucket at a time, and that is where the method gets its name from. At any given point of time, this method works with at most two hashing functions. The hash function changes its nature underneath dynamically and the hash table algorithms take care of using the right hashing algorithm for insert(), lookup(), remove() operations on a given key.
Linear Hashing uses the chaining or overflow bucket approach. This along with the fact that hash table size grows by exactly “one bucket” at a time are important facts about this method.
High Level Points about Linear Hashing
- We start with “N” as the initial size of the hash table where “N” is some power of 2. Note that “N” is the number of main hash buckets in the hash table and not the overflow buckets.
- Buckets are numbered through 0 to N-1.
- The hash function H(K) will first compute a bitstring R using the key K.
- The integer value corresponding to “I” LSB(s) from R is the bucket index B for a given key K.
- From points (1) and (4), it should be easy to infer that N = (2^I).
- Bucket B will be the result of hash function H.
- When a resize happens, we split a particular bucket B by creating a new bucket B*, and rehashing the contents of B between B and B*.
- A split pointer S indicates which bucket to split next.
- The split is done in a linear fashion where S points to bucket 0 at the beginning, and is incremented to point to the subsequent bucket upon every split.
- Note that only a single bucket is split, and the split is done in a linear order starting from very first bucket.
- Usually the trigger for a split is load factor which is equivalent to (number of items in the hash table)/(number of hash buckets). Load factor indicates the degree of fullness and the need for a hash table resize (bigger table).
- A threshold value of load factor L is set (say 75% or something). It implies that whenever the hash table is 75% full, the hash table will be resized. In case of any hashing scheme this would mean increasing the size of hash table by certain number of new buckets followed by a rehash. However, in case of linear hashing, this would imply:
- Creating a new bucket B* where B* = N + B ; N is the then size of hash table, and B is the bucket we are splitting.
- Rehashing the contents of bucket B (pointed to by S) between B and B*. This is what is meant by split.
- The hash function needs to embrace the fact that a particular bucket may have been split. This is where the second or alternate hash function comes into picture.
- One of the most important fact about Linear Hashing that distinguishes the technique from its counterparts is “the bucket that is split is not necessarily the bucket that overflowed“.
- The split is done in a linear bucket number order. The trigger for split can be anything. It may even be “every time we attach an overflow bucket to a particular bucket’s chain, we split“. But yes, the bucket that we will split will always be the one pointed to by S which may not be the bucket that just overflowed.
- This is completely different from extendible hashing technique where we always split the bucket that overflowed. For the readers who don’t know about extendible hashing, don’t worry about it. I will cover that as a follow up to this post.
All of the above mentioned points will definitely become clear further in this post.
We will use MOD as hash function, and integers as the keys for the hash table.
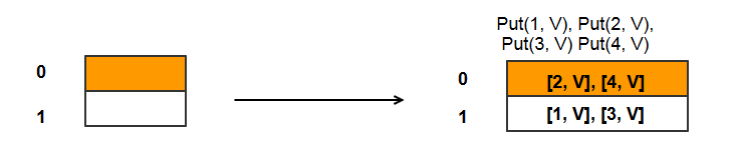
Let’s start with a simple example where the hash table has 2 buckets numbered 0 and 1. Let’s have a restriction that each bucket can store 2 records (KV items) before we chain out an create an overflow bucket. Similarly each overflow bucket will store only 1 record before we create and link another overflow bucket to the chain.
Following operations are carried out:
- Put (2, Val) => bucket index = H(2) = 2%2 = 0
- Put (1, Val) => bucket index = H(1) = 1%2 = 1
- Put (3, Val) => bucket index = H(3) = 3%2 = 1
- Put (4, Val) => bucket index = H(4) = 4%2 = 0
Let’s go back to point (4) where it is mentioned about the usage of “I” LSBs from the hash function to determine the bucket index. Remember that:
- The hash table N is in powers of 2.
- For the current example, we are using (key%N) as the hash function and integers as keys.
- N=2 => I=1.
These three things tell us that bucket index B for a given key K is really the LSB of integer key K. Let’s elaborate on this further by using the binary representation of the keys:
- Key 2 = 00000010, Key 4 = 00000100
- Key 1 = 00000001, Key 3 = 00000011
- The highlighted LSB in the binary representation of these keys is really the bucket index, and also the result of hash function H() as shown above.
The highlighted bucket in the diagrams below represents the bucket pointed to by S.
Get(2) => H(2) = bucket 0
Let’s look into split(). For that, we first establish that :
- S currently points to bucket 0.
- A split() will be triggered by an overflow implying that every time we create and link an overflow bucket to the overflow chain of bucket B during a Put() operation, we split the bucket pointed to by S before returning from Put().
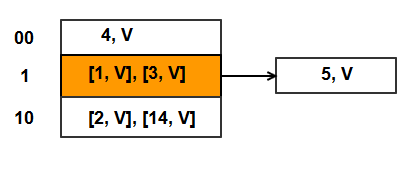
To trigger split, let’s do one more Put()
- Put (5, Val) => bucket index = H(5) = 5%2 = 1. Bucket 1 is full. So create an overflow bucket and store this KV pair in this new bucket.
- Link the new overflow bucket to the chain of bucket 1.
- Also, because we detected an overflow, we will split bucket S, which is bucket 0.
Split of bucket 0 (B).
- Create a new bucket N + B, which is bucket 2 as N is currently 2 and B is 0. This is the third bucket in hash table.
- B = 0 and B* = 2.
- Rehash items in B between B and B*.
- This is done using an alternate hash function H1(key). This is because we no longer have 2 buckets in the hash table and so “I” can’t be universally 1.
- The hash function needs to consider one more bit. Hence there is a need for alternate hash function that is aware of this fact.
- Because H() is key%N, H1() can be key%(2*N) since now we need 2 bits instead of 1 to determine the bucket index.
- Bucket 0 has keys 2 and 4.
- H1(2) = 2%4 = bucket 2, H1(4) = 4%4 = bucket 0
- 2 = 00000010, 4 = 00000100. Hence key 2 moves to bucket 10 (integer value 2) and key 4 remains in bucket 00 (integer value 0).
- Rehash done !!
- Increment S. S now points to bucket 1.
- Hash table now has 3 buckets numbered 0, 1, and 2
Let’s talk further about split().
Put(14, Val) = H(14) = 14%2 = 0. Hence key 14 goes to bucket 0. Wait !!, something is wrong here. Bucket 0 was just split into buckets 00 and 10. This tells us that we might be mapping the key 14 to incorrect bucket since H() only considers 1 bit. It is possible that 14 maps to the split image of bucket 0 which is bucket 2.
Get(2) => H(2) = bucket 0 which is incorrect because key 2 has been moved to a different bucket as a result of split of bucket 0. Hence, we need to use the second hash function to correctly lookup the key.
H1(2) => 2%2 = bucket 2
Hence, for insert () and lookup () into buckets that have been split, we need to use the second hash function H1().
H1(14) = 14%4 = 2. Alternately, 14 = 00001110. So key 14 goes to bucket 10 (integer value 2).
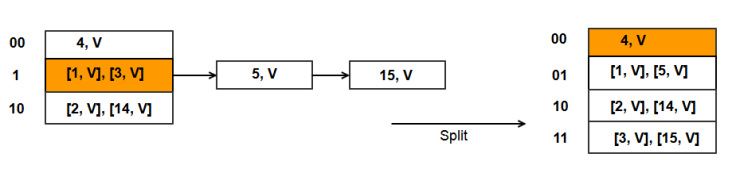
Put(15, Val) = H(15) = 15%2 = 1. Alternately 15 = 00001111. Hence key 15 goes to bucket 1.
Wait !!. Why are we not considering H1() for key 15 ? It is because the result of H() is bucket 1 which hasn’t yet been split. So to map key 15, hash function will consider only 1 bit. Hence the use of H() is sufficient.
- We insert 15 in an overflow bucket.
- Split bucket S, which is bucket 1.
Split of bucket 1 (B):
- Create a new bucket N + B, which is bucket 3 as N is currently 2, and B is 1.
- B = 1 and B* = 3.
- Rehash items in B between B and B*.
- Bucket B and its overflow buckets have keys 1, 3, 5, and 15.
- As B* is the fourth bucket in the hash table, we use 2 bits from the hash function H(). Hence we use the alternate hash function H1() where H1() = key%(2*N).
- H1(1) => 00000001 = bucket 01 (integer value 1) which is also equal to 1%4.
- H1(3) => 00000011 = bucket 11 (integer value 3) which is also equal to 3%4.
- H1(5) => 00000101 = bucket 01 (integer value 1) which is also equal to 5%4.
- H1(15) => 00001111 = bucket 11 (integer value 3) which is also equal to 3%4.
What has happened ? We started out with 2 buckets 0 and 1. Both the buckets were split, and the hash table size grew to 4 buckets. This completes a single round of linear hashing.
At the end of a single round of linear hashing, all the N buckets we started with would have been split, and the size of hash table would be 2*N or doubled (but only 1 bucket at a time). S, the split pointer is reset back to bucket 0, and our H() becomes key%4. Since the hash table size is now 4, it tells that hash function needs to consider 2 LSBs for determining the bucket index. So “I” is now equal to 2.
This further tells that when we reach a point of splitting a bucket, H1() would be key%(2*4). In other words, instead of 2, 3 LSBs would be considered by the hash function to determine the bucket index.
Another round of linear hashing will start when bucket 00 (bucket 0) will split into buckets 000 and 100 respectively.
Put(8, V), Put(12, V).
The Put() operation for key 12 causes an overflow in bucket 0. Hence we need to split the bucket pointed to by S, which in this case happens to be bucket 0.
- H(12) => 12%4 = 0. Alternately 12 = 00001100
- H(8) => 8%4 = 0. Alternately 8 = 00001000
Split of bucket 00
- Create bucket N+B => 4 +0 = 4
- B = 0, B* = 4
- We no longer have 4 buckets in the table. We are adding the 5th bucket. Hence, need to use 3 bits from the hash function.
- Rehash:
- H1(4) => 4%8 = 4. Alternately 4 = 00000100. This gives bucket 100 (integer value 4).
- H1(8) => 8%8 = 0. Alternately 8 = 00001000. This gives bucket 000 (integer value 0).
- H1(12) => 12%8 = 4. Alternately 12 = 00001100. This gives bucket 100 (integer value 4).
This round of linear hashing will continue until buckets 00, 10, 11 are split, and the table size at the end would be 8 buckets. H() would be key%8 and H1() would be key%(2*8).
This completes the introductory explanation to linear hashing method. I would like to complete the post by giving pseudo code for insert() and lookup() algorithms.
insert(K,V)
{
B = H(K);
if(B < S)
{
// bucket B has been split, so use H1() for correct bucket
B = H1(K);
}
hash_table[B] = <K,V>;
if(split_condition true)
{
split(bucket S);
}
}
lookup(K)
{
B = H(K);
if(B < S)
{
// bucket B has been split, so use H1() for correct bucket
B = H1(K);
}
V = hash_table[B];
return V;
}
The above pseudo code obviously glosses over creating and linking an overflow bucket during insert(), and searching through the overflow chain during lookup().
One important thing to note here. My examples kind of unintentionally show that when a bucket B is split and its contents are rehashed between B and B*, we seem to get rid of all the overflow buckets in the chain of bucket B. This is not true, and just happens to be the case here because of the keys I used in my examples. So, please do not go by the assumption that rehashing will get rid of the overflow chain. It is purely dependent on the key.
References:




Thanks for the great introductory. perhaps some animations or complementary videos could facilitate the understanding, although the text was fairly understandable.
I guess there is an errata in the following line (where I indicated by the asterisk):
H1(15) => 00001111 = bucket 11 (integer value 3) which is also equal to **3%4**.
LikeLike
Hi Novin,
Thanks for taking time to read the post and commenting. I do agree that some complimentary stuff would have been useful in addition to text and diagrams.
I am having trouble in finding out the problem in the particular line you pointed to. Can you please give some insight into the issue you were referring to? Are you saying we are incorrectly rehashing key 15 to bucket 3 or something else?
PS: Sorry for a delayed response. I have been off the grid for quite some time. Just got back.
Thanks,
Siddharth
LikeLike
Very clear explanation! Thank you so much !!
LikeLike